Placing N queens in N x N Chess board

Problem

In $N \times N$ chess board, you have to arrange N queens such that they do not interfere each other. Following is how you define interference of queens. 

1. Two queens cannot be on the same diagonal 

2. Two queens cannot be in same horizontal or vertical line 

3. Queen can jump like a knight. So, two queens cannot be at a position where they can jump two and half steps like a knight and reach the other queen. 

You should return the possible ways to arrange N queens on a chess board. 

First of all, we first need to understand how a queen move. Queen move four difference directions. (See Figure 1. for better understanding)

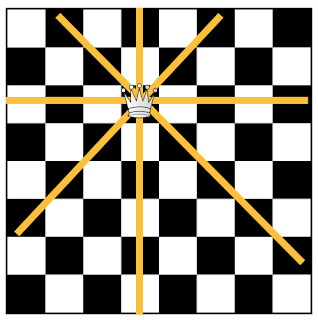Figure 1. Example of Queen's move

1) Left to right: this makes any row occupied by a queen unfit for other queens.
2) Top to bottom: this makes any column occupied by a queen unfit for other queens.
3) Top left to bottom right: this makes, any diagonal line occupied by a queen unfit for other queens.
3) Top right to bottom left: this makes, any second diagonal line occupied by a queen unfit for other queens.


Now, all we need to do is iterate over the NxN from top left (0,0) to bottom right(N-1,N-1), check for the following four facts stated above to determine whether a queen can be placed for current position x, y. (See Figure 2)

Figure 2. Placing queens from the left columns to right columns

To store the information of whether row, column, diagonal, second diagonal is occupied, we can use arrays.

Only trick thing is finding the right diagonal and second diagonal line given x,y.
For this, we need the array with size of $2N$. For diagonal, $x+y$ can find the position of the diagonal line the current position is on.

However, we need to be creative to find the second diagonal line for current x, y position.

We can use the following rules. (You can make up your own rule as long as it can find the correct second diagonal line.)

- If $x \ge  y$, position, $P = x-y$;
- if $x  \lt y$, position, $P = (y-x) + (N-1)$,  assuming both x, y starts from 0.

Update (29.06.2016): I made a silly mistake last time that there is only one way to place the queens, which always start from (0, 0).

This approach was wrong. We need to use all the possible ways to place the queens through the Depth First Search. The following is the additional explanation to find the ways to place the queens once the basic mechanism to mark the occupied verical/horizontal/diagonal rows.

DFS with backtracking, $O(N \times N!)$

DFS search starting from X = 0 to X = N-1 will be necessary to check if N queens can be placed.
For each X, we choose x $\in 0..N-1$, place the queen and move onto the next x to place the next queen.

There are N! possible search for chosen x in X=0 with depth of N. Therefore, time complexity of this algorithm will be $O(N \times N!)$.

Backtracking will be necessary to move up to the previous level and check another path.
Here is the complete code.

Update (June 18 2019): Solved this problem again and found that I don't have to keep the array representing the board. Instead, I just keeps coordinates of queens and compare a candidate coordinate to see if it intersects with existing coordinates. This way is simpler.

Check out the solution in python for this approach

C++ solution with array approach 

Practice statistics:

09:43: to think up the algorithm and write the code. (had a flaw, missed out the diagonal line from top-right corner to left bottom corner.)
20:00: to fix up the solution (couple of typos. This should not happen)


Python solution with new approach

Statistics for June 19 2019
- 25 mins: to think about algorithm
- 29 mins: write up the code but not tested.
- 10 mins: review the code and fix up silly initialization