How to find a sequential sub array which has the biggest sum [reviewed]

Problem

Given a number array, including positive and negative numbers, the question is to find a sequential sub array which has the biggest sum and the time complexity is $O(n)$,

For example, [1,-2,3,10,-4,7,2,-5] is an array, and the sub array [3, 10, -4, 7, 2] has the biggest sum which is 18.



This question is quite similar to "Finding the sequential sub array totaling the given number".
If you did not read this. I recommend you to do so before continue.

Difference is that there is no fixed length, N for the sub array and no given sum, S.

However, we can adopt the same strategy as in "Finding the sequential sub array totaling the given number" with the minor modification.

Take a look at the following illustration.

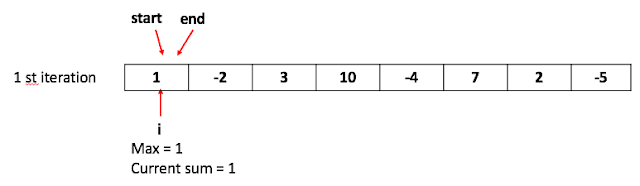Figure 1. Initial iteration
As you can see in Figure 1. we use two pointers, start and end to remember the latest max sub array.
Max is to remember the sum of the sub array,

We also keep track of the sum of all numbers up to the current position, i as well.

From this time on, we keep scanning the next element in i th position and check if the current sum up to i is larger than the last max value and make the following decisions:

Case 1) $\text{current sum }\gt \text{ max}$ : in this case we move the "end" pointer to i th position and replace the "Max" with the current sum.

Case 2) $\text{current sum }\lt \text{ max}$: we simply ignore the i th position element. No update to "end" and "Max". We just move on. However, we still need to update "Current sum".

Case 3) $\text{current sum }\le \text{ 0}$: This is an edge case. If current sum up to i become zero or negative value. We know that adding any elements up to i th position would not any value to the final sub array. In this case, we simply move both "start" and "end" to i+1 th position in the next iteration.

Don't forget to reset the current sum so that we start suming up numbers from i+1 th position as show in Figure 2, 3.
Figure 2: Special Case when current sum $\le$ 0

Figure 3: After resetting "Start" to i+1
Overall running time is still $O(N)$.

Here is the complete algorithm.



Practice statistics

15:30 : to hand-wrote the code on the paper
10:06.96: to code in the IDE.
04:11.44: to write the test case and validate the code


UPDATE(2019-07-26): solved the problem again.  Did not think of the case to move Start pointer.

Here is a python version of solution:


Practice statistics:

17:00 to write up the answer
Had to fix the logic error afterward. This should not happen.

Comments

Post a Comment

Popular posts from this blog

Planting flowers with no adjacent flower plots

Image
Problem Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die. Given a flowerbed (represented as an array containing booleans), return if a given number of new flowers can be planted in it without violating the no-adjacent-flowers rule  Sample inputs  Input: 1,0,0,0,0,0,1,0,0  3 => true  4 => false  Input: 1,0,0,1,0,0,1,0,0  1 => true  2 => false  input: 0  1 => true  2 => false  public boolean canPlaceFlowers(List flowerbed, int numberToPlace) {  // Implementation here  }
Read more
  Given an array of  intervals  where  intervals[i] = [start i , end i ] , merge all overlapping intervals, and return  an array of the non-overlapping intervals that cover all the intervals in the input . Example 1: Input: intervals = [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6]. Example 2: Input: intervals = [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.   Constraints: 1 <= intervals.length <= 10 4 intervals[i].length == 2 0 <= start i <= end i <= 10 4
Read more

Find the maximum number of bomb that can be detonated

  Problem You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb. The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range. You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range.  These bombs will further detonate the bombs that lie in their ranges. Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb. Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So...
Read more