Planting flowers with no adjacent flower plots

Problem

Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die. Given a flowerbed (represented as an array containing booleans), return if a given number of new flowers can be planted in it without violating the no-adjacent-flowers rule 
Sample inputs 

Input: 1,0,0,0,0,0,1,0,0 

3 => true 
4 => false 
Input: 1,0,0,1,0,0,1,0,0 

1 => true 
2 => false 
input: 0 

1 => true 
2 => false 

public boolean canPlaceFlowers(List flowerbed, int numberToPlace) { 

// Implementation here 
}

Answer

Brute-force approach, $O(N \times N!)$


   The first idea that came to my mind after understanding this question was to use DFS to find the best possible way to plant the flowers.
  Using DFS with the backtracking, we can easily determine whether a given target number of flowers can be planted. However, this will potentially take $O(N \times N!)$.

This is way too slow, which led me to the next solution, which I was able to complete in 32 mins.


Dynamic programming, O(N)

 In dynamic programming, we need to:

  • 1. image the ideal solution, $S_{n}$, where n is the last pot in the flowerbed.
    • Given the restriction of consecutive planting, the possible max number of pots $S_{n}$ can be written as below: $$S_{n} = MAX(S_{n-1}, S_{n-2} + W_{n}$$ where $W_{n}$ is 1 if n th pot is plantable, - $\infty$.
  • 2. build up the loop from the beginning based on the ideal solution by filling in the $S_{i}$ following the formula below: $$S_{i} = MAX(S_{i-1}, S_{i-2} + W_{i}$$
  • 3. backtrace the solution by walking the array S if necessary

Linear search with preprocessing ( not working)


I could not come up with a better name so I stated merely what the algorithm does.
Instead of using DFS, we can preprocess to identify the available empty plot in the flowerbed.

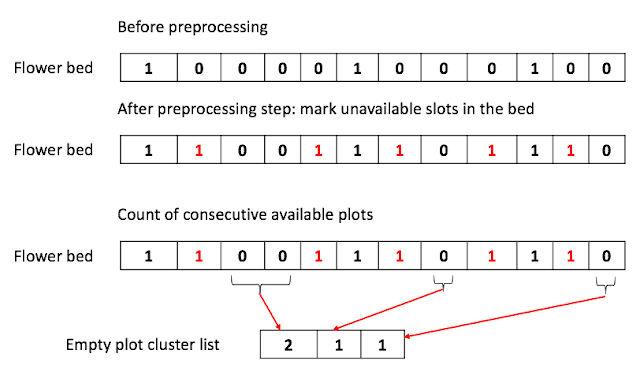Figure1. Example algorithm
Step 1: 
  As you can see in Figure 1, we first mark the all unavailable plot in the flower bed.  Any plots right before and after the occupied plot (marked as 1) are marked as 1.

Step 2:
   We now compile the list of consecutive empty plots (a cluster) by scanning the list.

Step 3:
    We now scan the list of clusters of empty slots and calculate the number of flowers to plants as below:
              Maximum number of flows to plants, M = $\lceil \text{number of empty plots} \rceil$

 We can continue to subtract the M from the target count while scanning the list of clusters.
This algorithm will take $O (N)$, where N is the length of the floor bed.

UPDATE(2022-06-28): After reviewing the original algorithm, I found that the original algorithm with the preprocessing has a bug. If empty slots after pre-processing are consecutive, we can't use the count as they are. We still need to find out how many plant we can plant for the consecutive slots.

Greedy algorithm approach


    The last way to solve the problem is to use a greedy algorithm. We try to plant the flower in the first available empty slot and continue to plant until there are no more available plots.
Surprisingly, this approach works in this case without causing the problem (draw it on the paper to see if it is true.)

This makes the code simpler than the previous approach with the same time complexity $O(N)$.


Here is the complete code for the greedy algorithm.
Here is the code for the linear search with preprocessing


UPDATE (2022-06-28): Solved the problem with the brute-force DFS. It is not optimal. 


18:45: for algorithm and bug-free code

I tried to do it with dynamic programming. This can run in $O(N)$ time. Much faster.

18:00 to write up the code.

Comments

Post a Comment

Popular posts from this blog

  Given an array of  intervals  where  intervals[i] = [start i , end i ] , merge all overlapping intervals, and return  an array of the non-overlapping intervals that cover all the intervals in the input . Example 1: Input: intervals = [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6]. Example 2: Input: intervals = [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.   Constraints: 1 <= intervals.length <= 10 4 intervals[i].length == 2 0 <= start i <= end i <= 10 4
Read more

Find the maximum number of bomb that can be detonated

  Problem You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb. The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range. You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range.  These bombs will further detonate the bombs that lie in their ranges. Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb. Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So...
Read more