K way merge problem

Problem

Assume you have very  K large arrays of integers stored in the Disk. It is so large that I would not fit into your computer memory.

You need to write the application that merge all K large arrays into sorted one list and store it in the disk.

Example, say the memory size, K = 6. Your program should be able to merge the following three arrays.
Note that each file has sorted list of integers.

  File 1 = {3,7,9,15,35};

  File 2 = {2,8,45,60,70,100};

  File 3 = {5,6,50,101, 110};

You need to write a program that merges the arrays into one array with all the numbers sorted in ascending order.

Given the fact that the machine does not have enough memory to load all three files,

we can load part of the files each time and sort in the memory and flush out to the buffer.

Brute force approach

We have the K partially sorted arrays loaded on the memory, all we need to do is to find the largest numbers among the first elements in the each arrays and store it in the output buffer.

After that we can move the pointer to the chosen array to the next element, we can repeat this process until we reach the end of one of K arrays. 

If that happens, we load the next chunk of the data into the array and start the process again.

What is the running time of this process? Let's break down the steps:

1) find the largest elements among the K elements. 

Brute force comparison will take $O(K^2)$ and Quick sort will take $O(K \log K)$. 

2) Loading the files in to the memory.

For simplicity, let's assume it is the same as reading each element one by one, thereby running in $O(N)$.

We will perform the step 1, for N elements, where N is the total number of integers stored in K files.

Total running time will be $$( N \times K \log K)$$

Heap approach

Can we do better?

Yes, we can use  Heap data structure to sort the K elements. Heap has the following properties.

- Adding element: $O( \log K)$
- Extracting element: $O( \log K)$.

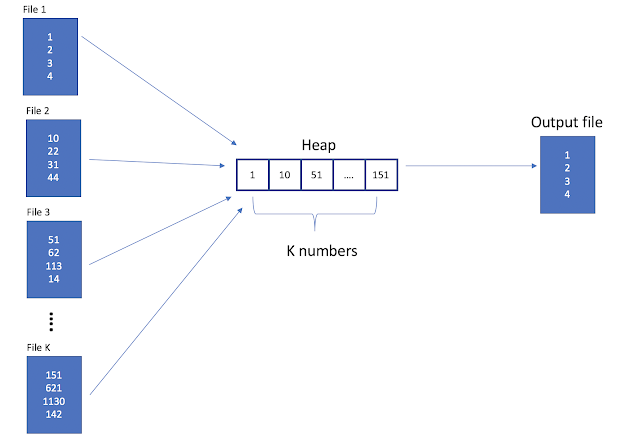K way merge using MinHeap

It guarantees the smallest element stays always on the top.

This will make the Step 1 in the "Brute force approach" run in $O(\log K)$.

Therefore total running time will be $$O(N \times \log K)$$.


Here is the complete code.



Practice statistics:

3hrs: to write the code (spent most of time parsing the input data due to lack of solid assumptions)
           had a flaw in the heap implementation. Need better review practice

UPDATE(2019 06 26): solved this problem in python and took simpler approach by skipping the reading the number from file but implemented the flushing to the file part.

Here is the complete code in Python




Practice statistics:

29:00: to think of algorithm and write up the code without testing
10:00: to fix the typos and minor bugs (should not happen next time)