Finding the sequential sub array totaling to the given number[reviewed]

Problem

Given an array of integer A = {23, 5, 4, 7,2, 11}, and the length N, and target sum, S, write the algorithm that tells whether the sub array $A_{sub}$, where $\sum_{i=k}^p A_{sub} (i) = S$.

For example, If N = 3, and S = 13, it should return sub array, {4,7, 2}.


Given the requirements to return the sub array of sequential numbers whose sum equals to S, we can use a  "Queue" like buffer with size of N while iterative over the numbers in the array, S.

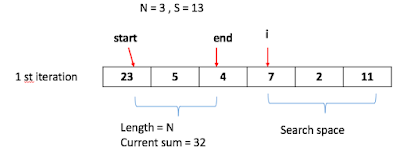Figure 1. Initial settings 

As shown in Figure 1, we initialize the two variable, "start" and "end" to 0 and N-1 respectively.
Of course, we should check if array A's size is larger than N, and compute the sum of A[0] ... A[N-1] and store it in Current sum.

The actual search start from N th element in the array.

If the current sum is not equal to S, we shift the current queue starting from "start" to "end" by 1.
Accordingly, we adjust the current sum as below:

    1. Subtract A[s] from the current sum.
    2. Add A[i] to the current sum

Figure, Second iteration after shifting by 1.

All we need to do is to repeat this process until either we reach the end of array, A or found the position, where current sum equals A.

Overall running time of this algorithm will be $O(N)$.

Here is the complete code running in $O(N)$



Practice statistics

13:18.88 mins : to hand wrote the code.
5:45.03 mins: to write up in the IDE.


UPDATE(2019-07-26): solved the problem again.

Here is a solution in python.


Statistics:

9:00 for algorithm

11:00 to write up the code and fix two logic error after runnig the code. review the code before running. Need to be more careful.