Given dictionary words, find words matching the given pattern

Problem

Input was given as 

List dict = new List();

that contains a list of 10000 words. Find all the words that match the given pattern without regular expressions.

Ex: You are given a pattern like (h*t). The words matching it would be (hot, hit, hat, etc.)

This problem is similar to "Finding the words by ranking" in that it utilize Trie data structure to store the words. Only difference from "Finding the words by ranking" case, is that the Trie we implement for this question does not keep the list of words by ranking.

Instead, it keeps either empty string in case of the current node is not leaf node or the word. Figure 1. illustrate the structure of the Trie.

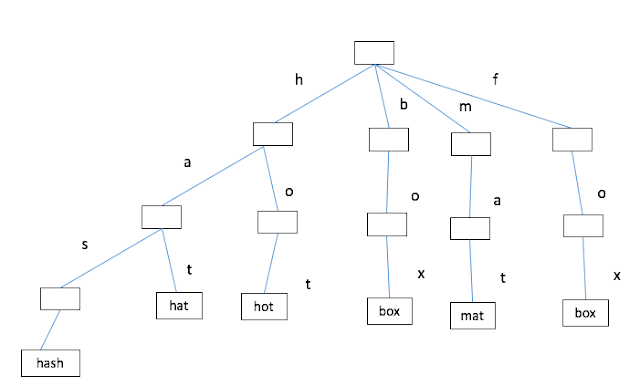Figure 1. Trie example

After building the Trie, we can perform the DFS to find the word matching the given pattern.

If pattern contains "*", we search all the children of the node. We can pass the std::vector to the DFS method to store the found words.

Running time of this algorithm will be as blow:

- Building Trie from the N words: $O(K \times N)$, where K is the longest word in the input list.

- Searching Trie for the given pattern, $O( K \times M^T)$, where K is the length of the pattern, T is the number of "*" in the pattern and M is the number of children in each node.

This is the worst case running time when input pattern is $$"****"$$
With one "*", in the pattern with the length K, the running time will be $O( K \times M)$.

Here is the complete code.



Practice statistics:

25:49: to write up the solution without building Trie. (initial data structure had a flaw)
10:31: to write up the logic building the Trie.
10:00: to fix up the flaw, which returning the non-existing words. Made the Trie's leaf has the value and intermediate node does not have value.


UPDATE ( 2019-06-03):

Retried the same question again. Not sure why I used Trie. Building the Trie alone already takes O(N) and search the list will take O(N) any way depending on the number of '*' in a search pattern.

This means simple brute-force search can be legitimate solution, which takes O(KN), where K is the longest words in the dictionary and N is the number of words in the dictionary.

I wish there is a faster way like $O(log n)$.  I did not find the solution yet.

Here is a python solution implementing


end