Finding nth expressible numbers [reviewed]

Problem

Given set of the prime numbers, P , find the nth biggest number that can be expressed with the numbers in P.

  e.g. prime set = {2, 3} , expressible numbers = { 1, 2, 3, 4, 6 .. } , Given N = 3, the 3rd largest expressible number is 3.


Let's see how we can list expressible numbers, given two prime numbers: 2,3

{ 1, $1 \times 2$, $1 \times 3$, $2 \times 2$, $2 \times 3$, $3 \times 2$, $3 \times 3$, ...}

Starting from each numbers, we multiply either 2 or 3 to produce the next numbers repeated. If we draw this in the graphs, it would look like this.

1. Finding the pattern

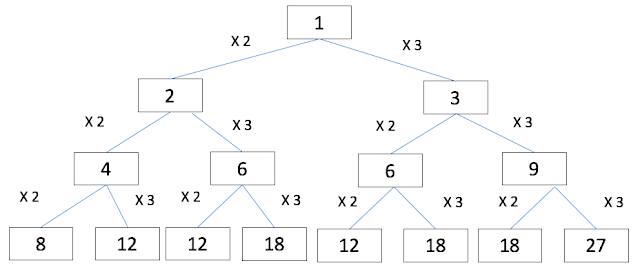Figure 1. Expressible number tree.
It seems we can do BFS to produce the numbers. Only thing we need to do is to store the numbers each time for later use.

2. Duplicate numbers

As you can see this way of producing the expressible numbers generate the duplicate numbers in each level in the tree,

Do we need to worry about that considering that we need to find N th largest numbers?

We can use HashTable or Set (in C++) to avoid adding the duplicate numbers. Does it worth? I don't think so.

3. When to stop

Now, we need how to produce the expressible numbers. One question that would strike your mind would be "when should I stop?". Given input, N, we can stop between 2N and 3N, considering the duplicate and possible "out of order" situation. Both 2N and 3N results in the same running time.
Let produce 3 times more numbers than N.

4. Sorting the numbers and find Nth largest numbers

Now we have 3* N expressible numbers. Last thing we need to do is to sort them in ascending order.
Question states that "find Nth largest numbers", but it seems to be misstated, it would be Nth smallest numbers from the beginning of the array.

Given sorted numbers, we can literate over the list until we encounter the Nth smallest element.
One caveat is that the array contains duplicate numbers. Therefore, we need to keep track of the unique numbers we encounters and return 10th unique number, which may not be in 10th position in the array

Over all running time of this algorithm is $O( N \log N)$, where N is the input parameter due to the sorting in the step 4.

Here is the complete code, running in $O(N \log N)$



Practice statistics:

5:08 : to come up with the vaguely right algorithm.
22:42: to hand-wrote the algorithm in the paper
16:36: to implement the useless MinHeap, which was not necessary at all.

Initial algorithm was completely wrong. Overlook how the primes should be multiplied.

Afterward, fixed the algorithm and achieved $O(N \log N)$ running time


UPDATE(2019-07-26): solved the problem again with python. Could not come up with algorithm in 10 minutes.

Here is a python version of solution.


Statistics:

15:00 to write the code.
3:00 to debug the code. made silly typo for variable and forgot the usage of deque()

Comments

Post a Comment

Popular posts from this blog

Planting flowers with no adjacent flower plots

Image
Problem Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die. Given a flowerbed (represented as an array containing booleans), return if a given number of new flowers can be planted in it without violating the no-adjacent-flowers rule  Sample inputs  Input: 1,0,0,0,0,0,1,0,0  3 => true  4 => false  Input: 1,0,0,1,0,0,1,0,0  1 => true  2 => false  input: 0  1 => true  2 => false  public boolean canPlaceFlowers(List flowerbed, int numberToPlace) {  // Implementation here  }
Read more
  Given an array of  intervals  where  intervals[i] = [start i , end i ] , merge all overlapping intervals, and return  an array of the non-overlapping intervals that cover all the intervals in the input . Example 1: Input: intervals = [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6]. Example 2: Input: intervals = [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.   Constraints: 1 <= intervals.length <= 10 4 intervals[i].length == 2 0 <= start i <= end i <= 10 4
Read more

Find the maximum number of bomb that can be detonated

  Problem You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb. The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range. You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range.  These bombs will further detonate the bombs that lie in their ranges. Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb. Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So...
Read more