Moving zeros in the array to the left

Problem 

Push all the zero's of a given array to the end of the array. In place only. Ex 1,2,0,4,0,0,8 becomes 1,2,4,8,0,0,0.

No additional allocation of array is not allowed. Everything should happen in place.

Simplest approach, but wrong

The easiest way is to allocate the new array that has the same size as the original input and scan the original input array can copy only non-zero numbers into the new array.

After that, we can set the rest of the unoccupied array to zero. The running time of this algorithm is $O(N)$

In place approach (Updated on June 19 2019)

To solve this problem in place, we need two pointers: current, and zero.

current: points to the current element to examine to check if it is zero
zero: points to the position of left most zero from consecutive zeros if present. If not, zero will be N, where N is the size of the input array.

Two invariants will be guaranteed by these two-pointers.

1. all elements on the left side of the cur pointer are non-zero
2. all elements on the right side of zero pointers are zeros.

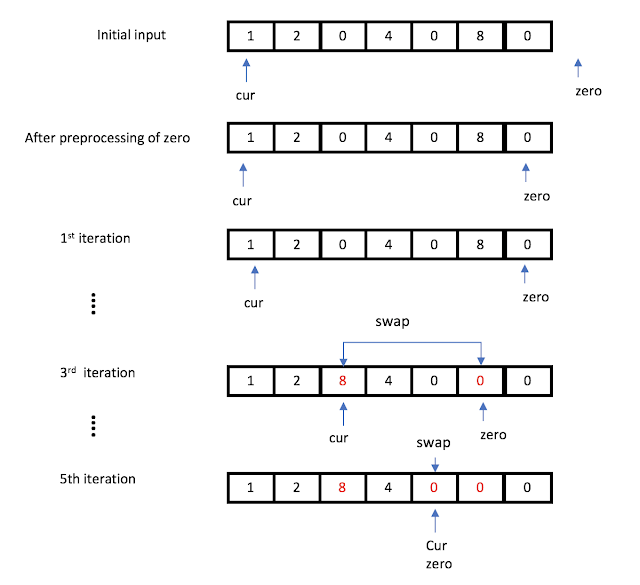
Take a look at Figure 1. 

To ensure the 2nd invariant, we do the preprocessing to find the correct position for zero pointers by scanning from the end of the array. In the example above, zero will points 6 since it is left most zero from the end.

Once this is done, we iterate over elements in the array, $$A$$ and perform the following check:

        if $A[cur]$ equals 0:
            if $A[zero]$ equals 0:

              zero --

            else
             swap elements in current and zero position

             cur++ 

             zero--

        else
            move on to the next element (cur ++)

We perform this operation until cur and zero crosses each other.

The overall running time of this algorithm is $$O(N)$$.

Here is a new answer in python.




Practice statistics:

9:00: to write up the code. Overlooked the corner case
0:37: to run the code. found the bug later
5:00: to fix the bug.

Here is the old answer in C++. This uses a different algorithm.

Practice statistics

09:02: to come up with the algorithm and hand-wrote the solution

04:49: to write the code in IDE

02:16: to fix up the typo (1 typo) and write the test case.

UPDATE(2022-06-14): Solved the question again in python.  The original python solution had the bug where we could swap the zero with the non-zero value that the zero point is pointing to. This new algorithm handles that case.

13:00: to write the code

07:00: to write the complete test code