Finding out how many elements are larger than remaining elements [reviewed]
Problem
Given an array of elements, return an array of values pertaining to how many
elements are greater than that element remaining in the array.
e.g [3,4,5,9,2,1,3]
return [3,2,1,0,1,1,0]
Running time should be faster than O(N^2)
Brute-force algorithm to this problem would be comparing the $i th$ elements with the rest of the elements in the array to count the larger elements.
This approach would take $O(N^2)$, which is not optimal algorithm.
Counting the larger elements in the right size of $i th$ element is the same as the number of elements that needs to be moved to the left size of $i th$ element during the merge sort in sorting the element in descending order.
To be honest, it is not that intuitively obvious unless you understand how the merge sort works thoroughly.
Idea is that we can piggy-back our counting routine to the merge sort algorithm to the merge routine.
There is one caveat. That consider the following case:
In the first merge step, with 3 on the left and 4 on the right, we will increase the count of 3 by one.
We also will increase the count of 5 when merging with 9 as well.
Problem happens when we merge the two bigger array: the left array with {4, 3} and the right array with {9, 5}. If we only increase the count of the current element on the left array, only count of the 4 will increase by 1 as in Figure 2.
We should also increase the count of 3, by 1 as well since 9 is also the larger number on the right side of 3 as well.
Keeping that tricky case in mind, we can know implement the modified merge sort to solve the problem. Overall running time will be $$O(N \log {N}), N = \text{number of elements in input array}$$
However, the running time could take $O(N^2)$, if the input array is sorted in ascending order due to the routine updating the count of all elements on the left array. ( could take up to $O(N)$).
Here is the complete code.
In fact, we can avoid updating the multiple elements in line 30-31. In stead of sorting the numbers in descending order, we can sort the numbers in ascending order.
In this case, we can still update the counter when we encounter the larger number on the right size of partial array. However, we can update the count of the left element as blow $$\text{ count of left element += the count of right element + 1}$$
In that way, we can avoid updating the multiple elements through additional for-loop and overall running time will be always $$O( N \log N)$$
Here is revised code.
Practice statistics
22:46 : to hand-wrote the algorithm
17:37: to fix up the major logical flaw. Got updating the count wrong. Did not think of the case described in Figure 2.
UPDATE(2019-07-26): solved the problem again. Could not come up with the algorithm in 15 mins.
Had to spend another 10 mins to come up with algorithm using merge sort.
Initial implementation uses increment the count of left element by number of elements left on the right side of partial array. e.g ( for i th right element, len(right array) - r.
Later, I realized that I can just increment by count of right element + 1.
Here is a solution in python.
Practice statistics:
15:00: couldn't come up with the algorithm
10:00: finally come up with algorithm using merge sort.
10:00 : could not finish merge_sort function yet.
20:00 : to finish the coding and fix the bug.
Brute-force algorithm to this problem would be comparing the $i th$ elements with the rest of the elements in the array to count the larger elements.
This approach would take $O(N^2)$, which is not optimal algorithm.
Counting the larger elements in the right size of $i th$ element is the same as the number of elements that needs to be moved to the left size of $i th$ element during the merge sort in sorting the element in descending order.
To be honest, it is not that intuitively obvious unless you understand how the merge sort works thoroughly.
Idea is that we can piggy-back our counting routine to the merge sort algorithm to the merge routine.
There is one caveat. That consider the following case:
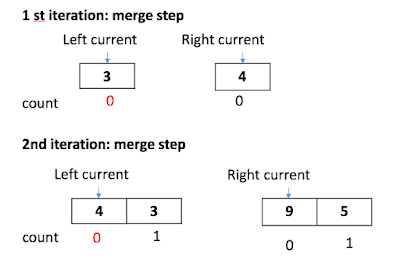 |
| Figure 1. First 2 merge steps in merge sort. |
We also will increase the count of 5 when merging with 9 as well.
Problem happens when we merge the two bigger array: the left array with {4, 3} and the right array with {9, 5}. If we only increase the count of the current element on the left array, only count of the 4 will increase by 1 as in Figure 2.
 |
| Figure 2. After 2nd merge steps. Incorrect & correct cases. |
Keeping that tricky case in mind, we can know implement the modified merge sort to solve the problem. Overall running time will be $$O(N \log {N}), N = \text{number of elements in input array}$$
However, the running time could take $O(N^2)$, if the input array is sorted in ascending order due to the routine updating the count of all elements on the left array. ( could take up to $O(N)$).
Here is the complete code.
In fact, we can avoid updating the multiple elements in line 30-31. In stead of sorting the numbers in descending order, we can sort the numbers in ascending order.
In this case, we can still update the counter when we encounter the larger number on the right size of partial array. However, we can update the count of the left element as blow $$\text{ count of left element += the count of right element + 1}$$
In that way, we can avoid updating the multiple elements through additional for-loop and overall running time will be always $$O( N \log N)$$
Here is revised code.
Practice statistics
22:46 : to hand-wrote the algorithm
17:37: to fix up the major logical flaw. Got updating the count wrong. Did not think of the case described in Figure 2.
UPDATE(2019-07-26): solved the problem again. Could not come up with the algorithm in 15 mins.
Had to spend another 10 mins to come up with algorithm using merge sort.
Initial implementation uses increment the count of left element by number of elements left on the right side of partial array. e.g ( for i th right element, len(right array) - r.
Later, I realized that I can just increment by count of right element + 1.
Here is a solution in python.
Practice statistics:
15:00: couldn't come up with the algorithm
10:00: finally come up with algorithm using merge sort.
10:00 : could not finish merge_sort function yet.
20:00 : to finish the coding and fix the bug.
Comments
Post a Comment