Find the combination of numbers making triangle [reviewed]

Problem

Find all triangle combination from a given array of integers.

For example, given array of integers, {8,7,3,2,5,6,1,4}, your algorithm should produce list of combinations that makes triangle.


First of all, we should remember than given tree numbers, a, b, c, triangle can be made when

a + b > c  (a < b < c)

If the input numbers are sorted in ascending order, we can easily the combination making triangle as below:

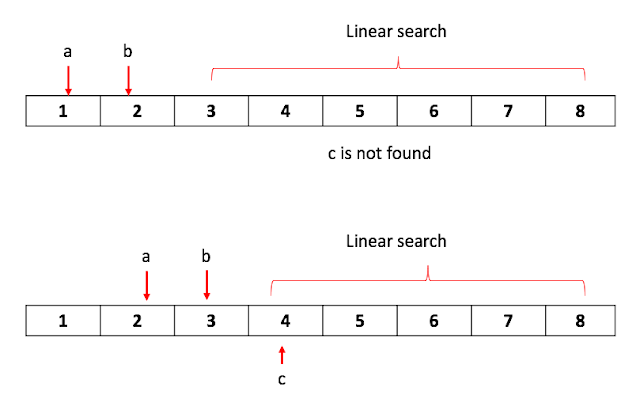Figure 1. Initial algorithm

1. Starting from the beginning of the array, choose for two numbers, a and b as shown in Figure 1.
   1-1. Among the rest of numbers, find the third number, c satisfying a+b > c.
2. Shift a, b by one, perform the step 2 (see lower picture in Figure 1).

Let check the running time of this algorithm.

Sorting: $O (N \log N)$
Step 1: $O (N^2)$  (Loop takes O(N) and sub step 1-1 will take O(N) )
Overall: $ O(N^2)$

If we can optimize step 1-1 using binary search, which runs in O(log N). We can bring down the running time to O( N log N). The binary search algorithm would be similar to what we wrote in H-Inex problem. We just need to find the last position of c meeting c < a + b. (See Figure 2.)

Figure 2. O( N log N) with binary search

Here is the complete code written in C++.



Someone might say that the code will take O(N^2) because of the step iterative over the found numbers and add the results to the vector.
It is just for the testing, we can simply remember the start and end in the input array and print out the result later.

Practice statistics

8 mins: to think up the algorithm
16:10 mins: to write up the code
4:35 mins: to verify the code (no typo this time)
4:54 mins: to uncover the logical mistake (regarding how to store the results)


UPDATE(2019-07-26):  solved the problem again. Came up with correct algorithm and complete the implementation on time. However, there was critical bug in the binary search code, which took more than 25 mins to find out after in-depth debugging.

Here is the solution in Python.


10:33.24: to come up with algorithm
15:08.58: to write the code
04:34.20: to review the code and fix syntax error

06:00: to fix the bug after running the code
18:28: to fix the bug in binary search.