Finding m missing numbers in the Array of size (n - m) [reviewed]
Problem
Array of size (n - m) with numbers from 1..n with m of them missing. Find all of the missing numbers in O(log n). Array is sorted.
example:
n = 8
m = 2
arr = = {1,2,4,5,6,8}
output = {3,7}
n = 8
m = 2
arr = = {2,3,4,5,6,7}
output = {1, 8}
As requested in the question, our algorithm should run in $O(\log N)$. It is lucky to know the required running time since it gives an idea of which algorithm you can choose to solve the question.
In many cases, no running time requirement is given. Therefore, keep in mind that we should aim for the fastest possible.
Given $O(\log N)$ running time requirement, we can easily think of using binary search. Problem is how we can use it and it is enough to solve the problem. In fact, we need to consider the following three cases.
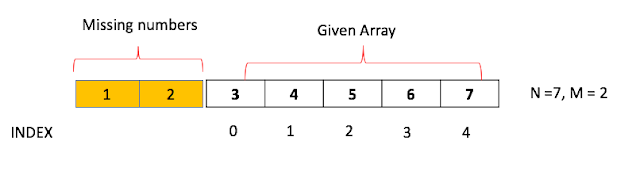
As shown Figure 1, if numbers are missing in the left side of array, the index, $i$ of the element in the beginning of array is not equal to $A[0] - 1$. It is an easy case to handle, we just need to add missing number from 0 to A[0]-1. (running time $O(M), M \lt N$)
UPDATE(2019-07-26): There is typo in Figure 2, it should be 5 instead of 7 in the given array.
As shown Figure 2, if numbers are missing in the right side of array, the index, $i$ of the element in the end of array is not smaller than to N. It is also an easy case to handle, we just need to add missing number from A[0]+1 to N. (running time $O(M), M \lt N$)
This case is a tricky case that we need to put most of our efforts. To achieve $O(\log N)$ running time, we need to use binary search to reduce the searching space by half. Here is the rough algorithm.
In this algorithm, we only ignore the half of the search space, if there is no missing numbers in the range, which means all integers in the range are consecutive.
As requested in the question, our algorithm should run in $O(\log N)$. It is lucky to know the required running time since it gives an idea of which algorithm you can choose to solve the question.
In many cases, no running time requirement is given. Therefore, keep in mind that we should aim for the fastest possible.
Given $O(\log N)$ running time requirement, we can easily think of using binary search. Problem is how we can use it and it is enough to solve the problem. In fact, we need to consider the following three cases.
Case 1) Left side of the given array has missing numbers
 |
| Figure 1. Missing numbers in the left side of array |
As shown Figure 1, if numbers are missing in the left side of array, the index, $i$ of the element in the beginning of array is not equal to $A[0] - 1$. It is an easy case to handle, we just need to add missing number from 0 to A[0]-1. (running time $O(M), M \lt N$)
Case 2) Right side of the given array has missing numbers
 |
| Figure 2. the right size of array has missing number. |
UPDATE(2019-07-26): There is typo in Figure 2, it should be 5 instead of 7 in the given array.
As shown Figure 2, if numbers are missing in the right side of array, the index, $i$ of the element in the end of array is not smaller than to N. It is also an easy case to handle, we just need to add missing number from A[0]+1 to N. (running time $O(M), M \lt N$)
Case 3) Numbers are missing among integers in the array
 |
| Figure 3. Numbers are missing among integers in the array. |
This case is a tricky case that we need to put most of our efforts. To achieve $O(\log N)$ running time, we need to use binary search to reduce the searching space by half. Here is the rough algorithm.
Search(s, e, A, m), s = start index, e = end index, A = input array, m = # of missing number
{
if (s>e or m = missing.size())
return
if e-s == 1 // only two elements are left to search
Add any missing numbers between A[s] and A[e]
return
h = middle of s and e
if A[h] - A[s] != h -s // numbers are missing between s and h
search(s, h, A, m) // search between s and h
if A[e] - A[h] != e -h // numbers are missing between h and e
search(h, e, A, m) // search between h and e
}
In this algorithm, we only ignore the half of the search space, if there is no missing numbers in the range, which means all integers in the range are consecutive.
The running time of this algorithm is $O(\log N)$
Based on the assumption that M is trivial compare the N, the total running time of handing all three cases stated above is as below: $$O(M) + O(\log N) + O(M) \approx O(\log N)$$
Here is the complete code running in $O( \log {N})$
Practice statistics
22:17 : to think up the algorithm and hand-wrote the algorithm (still did not consider the corner cases)
22:50: to write the code in the notepad and rethink the algorithm to consider the corner cases.
6:09: to add the test cases to main()
3:34: to fix up the typos through IDE.
Total time: 54:42 (too long)
UPDATE(2019-07-26): solve this problem again. Could not come up with a complete algorithm in 10 mins.
Here is a solution in python.
Practice statistics:
10:00: could not come up with solution.
15:00: to write up the solution.
5:00: to review code and fix two bugs (through running)
- condition to determine missing trailing numbers were wrong
- test code was putting wrong input variable.
Comments
Post a Comment