Finding the common ancestor in the tree - Part 2 [reviewed]

Problem

You are given a Binary Tree (not BST) along with two pointers to nodes somewhere in the tree.
Your algorithm should returns the pointer to the common parent to given nodes.

For example, in the following tree
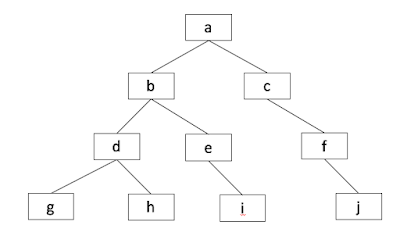Figure 1. Binary Search Tree example

The common ancestor of "d" and "f" is "a".

This is another variation of the "Finding a common ancestor in the tree problem"

Unlike the Binary Search Tree, Binary Tree does not offer the pointer to the parent, which makes this question trickier than Part 1.

However, basic algorithm is the same as the original problem in Part 1.

1. You need to know the depth of the given input nodes.
2. You need to chase up the parent nodes for given input nodes during the the comparison step.

Problem is how we can achieve these two things without the help of the parent pointer.

We can use DFS (Depth First Search) algorithm with additional Stack to remember the parents encountered during the search.
Basically, we can perform the DFS to first find the each node given as input. In doing so, we can keep track of the nodes that we encountered. If the backtracking happens, we can pop the node as well.

Once, DFS is done for both nodes, each of which takes O(N) time, where N is the number of nodes in the tree.
We also obtain two stack with list of parents DFS found while searching for the nodes.

Once this step finish, searching the common ancestor is quite straightforward. Only difference is that we pop the parent from the stack instead of referencing the parent pointer.

Here is the complete code running in O(N) as opposed to O( log N) in Part 1.



Practice statistics

40 mins: write up the code based on the algorithm (algorithm was right but implementation was wrong)
12 mins: to find the critical logical flaw in the code and fix up the typos through compilation

UPDATE(2019-07-29): Solved the problem again.

Here is rough algorithm: Given two target node, p1, p2.


  • search p1 in the binary tree while adding the parents encountered to p1_parents: $O(log N)$
  • search p2 in the binary tree while adding the parents encountered to p2_parents: $O(log N)$


  • iterate over two list from the end and find the common ancestor.  
         - check if both nodes are the same. If so, we found a common ancestor
         
           Case1: if the positions of two lists are different, only decrease the index of larger one
           Case2: if the positions of two lists are same, decrease both index by 1.

Overall, running time is O(N). N is the number of nodes in the tree.

Here is a solution in python.


Practice statistics

7:42: to come up with algorithm
14:00: to write the code
2.40: to review and fix a bug

9:00: to write the test code and fix a logical bug and typos (after running)

Comments

Post a Comment

Popular posts from this blog

Planting flowers with no adjacent flower plots

Image
Problem Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die. Given a flowerbed (represented as an array containing booleans), return if a given number of new flowers can be planted in it without violating the no-adjacent-flowers rule  Sample inputs  Input: 1,0,0,0,0,0,1,0,0  3 => true  4 => false  Input: 1,0,0,1,0,0,1,0,0  1 => true  2 => false  input: 0  1 => true  2 => false  public boolean canPlaceFlowers(List flowerbed, int numberToPlace) {  // Implementation here  }
Read more
  Given an array of  intervals  where  intervals[i] = [start i , end i ] , merge all overlapping intervals, and return  an array of the non-overlapping intervals that cover all the intervals in the input . Example 1: Input: intervals = [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6]. Example 2: Input: intervals = [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.   Constraints: 1 <= intervals.length <= 10 4 intervals[i].length == 2 0 <= start i <= end i <= 10 4
Read more

Find the maximum number of bomb that can be detonated

  Problem You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb. The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range. You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range.  These bombs will further detonate the bombs that lie in their ranges. Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb. Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So...
Read more