Finding the common ancestor in the tree - Part 1[reviewed]
Problem
You are given a BST (Binary Search Tree) along with two pointers to nodes somewhere in the tree.
Your algorithm should returns the pointer to the common parent to given nodes.
For example, in the following tree
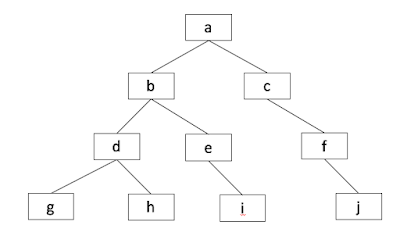 |
| Figure 1. Binary Search Tree example |
The common ancestor of "d" and "f" is "a".
There is another variation of this problem without a pointer to the parent, which is trickier than this one.
I will cover that problem in Part 2. Stay tune.
Ok, let think about the cases we need to consider.
Case 1: Both nodes given as input are in the same depth.
When both nodes are in the same depth, we can move up to the next parent if the current parent of nodes are not the same. In Figure 1, if g and i were the given input nodes, we can move up to the parent each time until we encounter "b", a common ancestor.
Case 2: Nodes given as input are not in different depth.
Problem happens when the input nodes are not in the same depth. Consider the case where b and g are the input nodes. their direct parent a and d are not the same. If we move up to the next parents, we ends up not finding the ancestor. In this case, we should move up only g's ancestor until it encounter b.
In other words, we should move up only the node whose depth is larger than the other until both are on the same depth or find the common ancestor.
Both cases are based one fact that we know the depth of given nodes already. Thanks to the parent pointer feature of BST, finding the depth can be calculated by tracking the parent in O( log N) time, where N is the number of nodes in the BST.
Afterward, comparing the ancestor with both Case 1 and Case 2 in mind will also take O (log N) time.
Here is the complete code running in O( log N).
Practice Statistics
21 mins: to code up the solution.
In other words, we should move up only the node whose depth is larger than the other until both are on the same depth or find the common ancestor.
Both cases are based one fact that we know the depth of given nodes already. Thanks to the parent pointer feature of BST, finding the depth can be calculated by tracking the parent in O( log N) time, where N is the number of nodes in the BST.
Afterward, comparing the ancestor with both Case 1 and Case 2 in mind will also take O (log N) time.
Here is the complete code running in O( log N).
Practice Statistics
21 mins: to code up the solution.
3 mins: to check for the typos or flaws. Could not find the simple typo until compilation. What a shame.
Comments
Post a Comment