Finding the number of ways to climb the stairs - Part 1

Problem

You are climbing a stair case. Each time you can either make 1 step or 2 steps. The staircase has n steps. In how many distinct ways can you climb the staircase ?

For example, If there are 3 stairs, there are three possible ways to climb them.

{1,1,1}, {1, 2}, {2, 1}

Your algorithm should print out the total number of ways to climb the stairs. (Optional: should also print out the different ways as above)

I will first start with the brute force approach, which does not give us ideal time complexity.
I will cover the better algorithm in Part 2. So stay tuned.

Given the two choices, 1 step or 2 steps, you can draws the Binary trees as below.

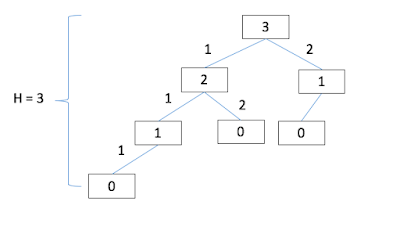Binary Tree to find ways to climb stairs
What we need to do is to perform DFS on the binary tree to find the case where node is zero and record the path.

Running time of DFS is O(M), where M = 2^N, where N is the number of stairs.
Therefore, running time of the algorithm is O( 2^ N).
Here is the complete code running in O( 2^N).


Above algorithm give us what we want but its running time O(2^N) is not ideal.
Can we do better ? I think so, let find a better algorithm in Part 2.

Practice statistics
23 mins: to write up the code
3 mins: to fix the typos through compilation.

Comments

Post a Comment

Popular posts from this blog

Planting flowers with no adjacent flower plots

Image
Problem Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die. Given a flowerbed (represented as an array containing booleans), return if a given number of new flowers can be planted in it without violating the no-adjacent-flowers rule  Sample inputs  Input: 1,0,0,0,0,0,1,0,0  3 => true  4 => false  Input: 1,0,0,1,0,0,1,0,0  1 => true  2 => false  input: 0  1 => true  2 => false  public boolean canPlaceFlowers(List flowerbed, int numberToPlace) {  // Implementation here  }
Read more
  Given an array of  intervals  where  intervals[i] = [start i , end i ] , merge all overlapping intervals, and return  an array of the non-overlapping intervals that cover all the intervals in the input . Example 1: Input: intervals = [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6]. Example 2: Input: intervals = [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.   Constraints: 1 <= intervals.length <= 10 4 intervals[i].length == 2 0 <= start i <= end i <= 10 4
Read more

Find the maximum number of bomb that can be detonated

  Problem You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb. The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range. You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range.  These bombs will further detonate the bombs that lie in their ranges. Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb. Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So...
Read more