Finding the number of ways to climb the stairs - Part 2

Problem

You are climbing a stair case. Each time you can either make 1 step or 2 steps. The staircase has n steps. In how many distinct ways can you climb the staircase ?

For example, If there are 3 stairs, there are three possible ways to climb them.

{1,1,1}, {1, 2}, {2, 1}

Your algorithm should print out the total number of ways to climb the stairs. (Optional: should also print out the different ways as above)

The previous solution in Part 1, was too slow. 

Using dynamic programming we can do better.

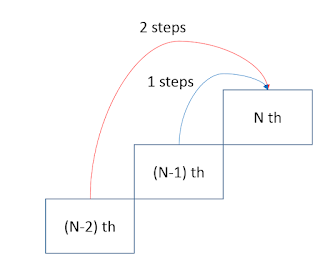
Instead of calculating the ways of climbing the stairs from the beginning of the staircase, we can calculate from the end of the staircases, Nth stair.

To reach the Nth stair, given the options of either 1 stair or 2 stairs each time, one should be from either the N-1th stair or the N-2th stair.

If there are n and m ways of reaching the N-1th and N-2th stair respectively.
The total ways of reaching the Nth stairs will be (n + m). We can write the algorithm as below:

W(N) = W(N-1) + W(N-2), where W(x) denotes the ways of climbing to the x th stair.

To use dynamic programming, we need to define the base case correctly.

W(1) = 1, W(2) = 2
After that, we can loop from 3 to N to find out W(N).  We should remember to store W(i-1) and W(i) after each iteration so that we can use them as W(i-1) and W(i-2) in the next iteration. This will take O(N), where N is the number of stairs.

In each iteration, we also use the list to keep track of the steps we took to climb to I th stairs as well. This takes up to  O(M), where M is the number of ways to climb to the Nth stair.
Therefore, the overall time complexity is O(MN). The following is the complete code.

	#include <list>
	#include <string>
	#include <iostream>
	using namespace std;
	void append_step(list<string> &l, char step)
	{
	list<string>::iterator iter;
	for (iter = l.begin(); iter != l.end(); iter++)
	(*iter).push_back(step);
	}
	void print_ways(list<string>&l)
	{
	list<string>::iterator iter;
	for (iter = l.begin(); iter != l.end(); iter++)
	cout<<(*iter)<<endl;
	}
	int find_ways_to_climb_stairs(int nSteps)
	{
	int cur;
	int W_2 = 1;
	int W_1 = 2;
	list<string> l_W1;
	list<string> l_W2;
	list<string> l_result;
	l_W1.push_back("2");
	l_W1.push_back("11");
	l_W2.push_back("1");
	for (int i = 3; i <= nSteps; i++)
	{
	list<string> l_cur;
	cur = W_2 + W_1;
	W_2 = W_1;
	W_1 = cur;
	l_cur= l_W1;
	append_step(l_cur, '1');
	append_step(l_W2, '2');
	l_cur.insert(l_cur.end(),l_W2.begin(), l_W2.end());
	l_W2 = l_W1;
	l_W1 = l_cur;
	l_result = l_cur;
	}
	print_ways(l_result);
	return cur;
	}
	int main()
	{
	int n = 5;
	cout<< " # of ways to climb "<< n <<" stairs: "<<find_ways_to_climb_stairs(n);
	return 1;
	}

view raw find_ways_to_climb_stairs2.cpp hosted with ❤ by GitHub

If the question is just to print out a total number of ways to climb the stairs, the following algorithm can do the job in O(N).

	int find_ways_to_climb_stairs(int nSteps)
	{
	int cur;
	int W_2 = 1;
	int W_1 = 2;
	for (int i = 3; i <= nSteps; i++)
	{
	cur = W_2 + W_1;
	W_2 = W_1;
	W_1 = cur;
	}
	return cur;
	}

view raw find_ways_to_climb_stairs_result_only.cpp hosted with ❤ by GitHub

Practice statistics
31 mins: to write up the code and fix the bug. Made a logical mistake and had to use the compiler to find it.

UPDATE (2019-07-27): solved the problem again in python.
It is the third time to solve this problem.

	class FindWaysToClimb:
	def find(self, N):
	matrix = [0 for i in range(N+1)]
	matrix[0] = 1
	for i in range(1, N+1):
	if i >= 1:
	matrix[i] += matrix[i -1]
	if i >= 2:
	matrix[i] += matrix[i -2]
	return matrix[N]
	finder = FindWaysToClimb()
	N = 3
	print("n = {}, ways = {}".format(N, finder.find(N)))
	N = 4
	print("n = {}, ways = {}".format(N, finder.find(N)))

view raw google_ways_to_climb_stairs.py hosted with ❤ by GitHub

Practice statistics

3:48: to write up the code
1:02: to review the code

UPDATE (2023-02-28): solved the problem again. This time I added the additional logic to print out the actual permutations.

	'''
	You are climbing a stair case. Each time you can either make 1 step or 2 steps. The staircase has n steps.
	In how many distinct ways can you climb the staircase ?
	For example, If there are 3 stairs, there are three possible ways to climb them.
	{1,1,1}, {1, 2}, {2, 1}
	Your algorithm should print out the total number of ways to climb the stairs. (Optional: should also print out the different ways as above)
	practice statics:
	10 mins: to come up with algorithm
	15 mins: to write up the algorithm with one bug
	1 min: to fix the bug
	10 mins: to add additional printing the ways
	'''
	import copy
	def find_ways_to_climb(num_steps):
	# initialize S0 and S1 to 1.
	S = [0 for i in range(num_steps + 1)]
	# initialize base case
	S[0] = 1
	S[1] = 1
	if num_steps < 2:
	return S[num_steps]
	for i in range(2, num_steps + 1):
	S[i] = S[i -1] + S[i -2]
	return S[num_steps]
	N = 3
	print( "unique ways for {}th stairs = {}".format(N, find_ways_to_climb(N)))
	N = 5
	print( "unique ways for {}th stairs = {}".format(N, find_ways_to_climb(N)))
	N = 6
	print( "unique ways for {}th stairs = {}".format(N, find_ways_to_climb(N)))
	# optional print out the ways.
	def find_ways_to_climb_with_print(num_steps):
	# initialize S0 and S1 to 1.
	S = [0 for i in range(num_steps + 1)]
	W = [[] for i in range(num_steps + 1)]
	# initialize base case
	S[0] = 1
	W[0] = [[]]
	S[1] = 1
	W[1].append([1])
	if num_steps < 2:
	return S[num_steps]
	for i in range(2, num_steps + 1):
	S[i] = S[i -1] + S[i -2]
	# merge the ways existing ways with 1 or 2.
	# 1 steps solutions
	for j in range(len(W[i - 1])):
	copied = copy.deepcopy(W[i-1][j])
	copied.append(1)
	W[i].append(copied)
	# # 2 steps solutions
	for p in range(len(W[i-2])):
	copied = copy.deepcopy(W[i-2][p])
	copied.append(2)
	W[i].append(copied)
	print(W[num_steps])
	return S[num_steps]
	N = 5
	print( "unique ways for {}th stairs = {}".format(N, find_ways_to_climb_with_print(N)))

view raw google_ways_to_climb_stairs_dp.py hosted with ❤ by GitHub

Practice statistics

10 mins: to come up with an algorithm

15 mins: to write up the algorithm with one bug

1 min: to fix the bug

1hr: to add additional logic to print the ways of climbing the stairs. Got messed up with the array generation.