Finding the predecessor in the binary tree.

Problem

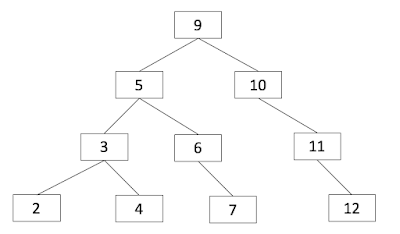
Given the root pointer of the binary tree and the pointer to the target node, find the predecessor of the target node.

For example, in Figure 1. the predecessor of  5 is 4.

In finding the predecessor, we need to consider two cases.

Case 1: the target node has a left child

Let's take the example of "5" in the tree, it has the left child, "3". In this case, the predecessor is the right-most node of the node, "3". if "3" has the right children. This is a simple case. In this example "4" is the predecessor.

Case 2: the target node does not have a left child.

However, if the target node is "6", things become a little tricky. In this case, its parent "5" is the predecessor. More specifically, the parent node of the target node if the target node is the parent's right child.
This means we need to keep track of the parent while we are searching.

Given the binary tree lacking the parent pointer, we need to have an extra pointer to store the lastly encountered parent. This will require a preliminary search to find the target node's parent.

To summarize, here are the steps we need to implement.

1) Find the target node from the root of the tree. Keep track of the parent node during the search.

2) Check if the target node suit Case 1 or Case 2 and find the predecessor.

Here is the complete code running in O(log N), where N is the number of nodes in the tree.

UPDATE(2022-06-12): Reviewed the problem again and found that I misunderstood the problem. The explanation I had was for finding the predecessor, not the successor.  Fixed the wording and the title.

I will add another example to find the successor of the target node in a separate post.

Also, prior solutions were wrong in that both solutions fails to find the predecessor in the parent tree.

The following is the complete solution in python.