Finding the closest node in the tree

Problem

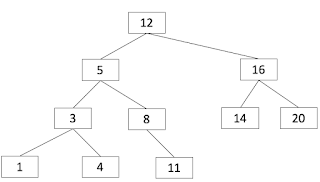
You are given the pointer to the binary tree and the value. You algorithm should find the pointer to the node that has the closest value to the given value.
For example, in the given tree in Figure 1.

If a 13 is given, your algorithm should return 12.

We can achieve $O( log {N})$ running time through binary search with the little tweak.
In stead of finding the exact match in the tree, we look for two closest numbers, one is smaller than the target number and the other larger than the target number.

Here is the rough algorithm

1) Given the pointers to min, max, cur, with the target, check if the cur node has the same value as the target. If so, return the current node.

2) check if the target is larger than cur node, if so, search the cur->left. Update the min pointer with the closer to the target.

3) check if the target is smaller than cur node, if so, search the cur->right. Update the max pointer with the closer to the target.

4) perform these step until, cur is empty. If we encounter empty. return the closer number to the target between min, and max nodes.

Here is the complete code running in $O( \log {N})$


Practice Statistics

21:47: to hand-wrote the code on the paper - need to work on neater hand writing
6:33: to type the code in the node pad
6:40: to verify the code.


UPDATE(2019-07-26): solved the problem in a different way. Looking at the previous answer, I don't we need to keep both min and max value at all. We just need to keep the closest value that had been seen.

For each value we encounter, we perform the followings.

Given target value, T.

If the current node's value, V is closer than previous closet, C, set the C to V.

Case 1: If V == T, we found the exact value, stop the searching.

Case 2: If V < T, we know that all the values on the left side of V are further away than V so only search right side of V.

Case 3: if V > T, we know that all the values on the right side of V are further away than V, so only search left side of V.

Here is the solution in python

Practice statistics

7:00: come up with a binary search
6:00: to write up the code
3:00: to fix typos
5:00: to write the test code (had to find the usage of abs() method)


UPDATE(2022-05-21): solved the same problem in a non-recursive way.

8:56: to come up with an algorithm
15:00: write up the code with the error. 
3:00: to fix up the error



Comments

Post a Comment

Popular posts from this blog

Planting flowers with no adjacent flower plots

Image
Problem Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die. Given a flowerbed (represented as an array containing booleans), return if a given number of new flowers can be planted in it without violating the no-adjacent-flowers rule  Sample inputs  Input: 1,0,0,0,0,0,1,0,0  3 => true  4 => false  Input: 1,0,0,1,0,0,1,0,0  1 => true  2 => false  input: 0  1 => true  2 => false  public boolean canPlaceFlowers(List flowerbed, int numberToPlace) {  // Implementation here  }
Read more
  Given an array of  intervals  where  intervals[i] = [start i , end i ] , merge all overlapping intervals, and return  an array of the non-overlapping intervals that cover all the intervals in the input . Example 1: Input: intervals = [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6]. Example 2: Input: intervals = [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.   Constraints: 1 <= intervals.length <= 10 4 intervals[i].length == 2 0 <= start i <= end i <= 10 4
Read more

Find the maximum number of bomb that can be detonated

  Problem You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb. The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range. You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range.  These bombs will further detonate the bombs that lie in their ranges. Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb. Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So...
Read more