Reading integer streams and return N th order statistics

Problem

Imagine you are reading in a stream of integers. Periodically, you wish to be able to look up the rank of a number x (the number of values less than or equal to  x).

Implement the data structures and algorithms to support these operations. 

The following methods need to be implemented.

// method to take new number x

void track(int x); 

// method to return the number of values that are less than or equal to x (not including x itself)

int get_rank(int x); 

Example:

Stream (in order of appearance): 5, 1, 4, 4,  5,  9, 7, 13, 3

get_rank(1) = 0

get_rank(3) = 1

get_rank(4) = 3

There are three possible ways, where first two uses the array and the last uses the binary tree.

Each approach has the advantages and disadvantages. Which solution is better would depend on which operation is more important or frequent than the other.

For this question, I will assume, get_rank() is called more frequently than track() itself.

Binary search approach using Array, $O(N)$ for track(), $O(\log N)$ for get_rank()

This approach scarifies the efficiency of track() for the sake of faster, get_rank() operation.

When the frequency of track(int x) method is less frequent than get_rank(), we can use array or std::vector to store the integers and sort the integers each time a new value is given.

Sorting the values each time takes $O(N)$ since it is basically inserting the new number in the middle of array, which causes the values after the new number shifted to the right.

For get_rank(int x) operation, we can use binary search to find the position of the largest values that is equal or less than x, which results in $O( log N)$ running time, where N is the number of values stored.

Here is the complete code in C++.

On demand sorting using Linked list, $O(1)$ for track(), $O(N \log N)$ for get_rank()

If we favor the efficiency of track(int x) operation, we can use linked list to store the values and defer the sorting until get_rank(int x) is called.

In this case, track(int x) operation is simply adding a new value to the end of the linked list, which runs in $O(1)$.

When track(int x) is called, we sort the values in $O( N \log N)$ time and linearly search x while counting the preceding values, which runs in $O(N)$.

Overall running time for track(int x) is $O( N \log N)$.
You can avoid sorting the numbers each time by remembering whether the numbers are sorted.
Say we keep the flag, bSorted. We reset the flag to false when track(int x) is called and set it to true after sorting the values.  If the flag is true when get_rank(int x) we can skip the sorting.

This approach is quite straightforward. Therefore, I would not show any coding example.

Binary search tree approach, $O(\log N)$ for track(), $O(\log N)$ for get_rank()

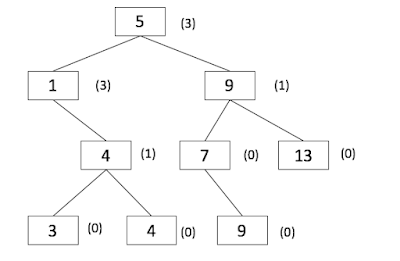
Last way is to use binary tree to store the values in descending order, assuming we are using balanced binary search tree.

In this case, track(int x) operation is to insert a new value to the binary search tree, which runs in O(\log N).

get_rank(int x) is to find the N th order statistics. It can be achieved through in-order search. However, it would take $O(N)$ time.

Considering that we are only interested in the values smaller than a given value, x, we can keep track of the number of nodes on the left side of the tree when adding the new element. (see Figure 1, for example tree).

Figure 1. Example binary tree with the left-side children counts

With this information present, we can now use the binary search for get_rank(int x) operation, which results in $O(\log N)$.

The last one is the most efficient but it would not be practical to use in the interview unless you are not required to write the code. Instead, you need to talk through the solution or write the pseudo code.

Balancing the binary tree will require the adjustment of the count of left side nodes in each node.
Unless you are confident that you can write both balancing routine less than 30 mins, I personally recommend you to go with the first solution and explain this solution as possible improvement.

The following code excludes the balancing the tree.




Here is python solution, this does not handle duplicate key correctly since it stop at the first occurrence of the matching key. We need better algorithm to handle duplicate key.