Finding the magic index in array, A

Problem

A magic index in an array A [0. . .n-1] is defined to be an index such that A[i]
= i. Given a sorted array of distinct integers, write a method to find a magic
index, if one exists, in array A.

FOLLOW UP

What if the values are not distinct?

Answer

This is another question I found interesting in the Cracking coding interview book.

Brute-force approach, $O(N)$

The simplest way to solve this problem is to scan the array, A from A[0] to A[N-1] looking for the index, i where A[i] = i.

However, this wouldn't be the answer to this question. This means the question is asking for a faster algorithm than $O(N)$. Possible $O(\log N)$ ?


Recursive Binary search approach, $O( \log N)$

Let's draw out the example array with the magic index at 3 with the size of 5. It would be like the below: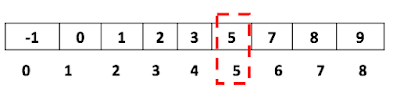

Figure 1. Example input
On the left size of the magic index, A[i] > i holds while i > A[i] holds on the right side of the magic index.

This gives enough information to perform the binary search following the algorithm below

Given, chosen half, h,

case 1) if A[h] == h, found the magic index

case 2) if A[h] > i, search the right size of index, h

case 3) if A[h] < i. search the right size of index, h

This algorithm will run in $O(\log N)$

If the values are not distinct, binary search will not work since both left and right sides of the magic index can have integers either greater than the index or less than the index.

Therefore, only linear scanning will work, which results in $O(N)$ time complexity
Here is the complete answer to the first part of the question.

Update (05.06.2016):

Initially, I thought only linear scanning will work if there are duplicate keys. However, I later realized that we can still perform the recursive search, which is marginally better than the linear scanning depending on the combination of the integers in the array.

Take the look at Figure 2, which presents array A, with duplicate integers.

Figure 2. For example case of duplicate integers, there are two magic indexes
There are three indexes in 2, and 8th in the array. However, we can no longer use the rules to determine whether to search the left or right half of the array anymore since the rules applied for the previous case do not hold anymore.

It is a major setback. However, there is the still a room for improvement. We should now search both sides of the array each time but we can still reduce the scope to search based on the following rules.

Given start, the starting position, and end the end position, the h, index splitting the array in half and A[h] the value in that position,

Rule 1) For the left side of the array, we now know that index h can't be the magic index anymore.
In choosing the new end index for search, we can choose the minimum of h-1 and A[h].
Therefore, we search between start and Min(h-1, A[h])

 Rule 2) For the right side of the array, we also know that index h can't be the magic index anymore.
In choosing the new start index for search, we can choose the maximum of h-1 and A[h].
Therefore, we search between Max(h-1, A[h]) and end

UPDATE(2022-06-24): This algorithm can't work if the negative values are allowed in the array. This is only valid if only non-negative values are in the array.

I would say the expected running time is faster than $O(N)$ since it is not guaranteed that we can reduce the search space each time considerably.
However, it will be faster than the linear search in practice.

The following code is modified to apply the two rules explained above.



Practice statistics
19:23: to write up the code
08:48: to realize the second question is for $O(N)$


** April 28 2019: Tried again in Python. Here is a solution in Python


Practice statistics

21 mins: to write up the code
5 mins to write up the answer to the second question is for $O(N)$

UPDATE(2022-06-24): Solved the problem again with the binary search with the distinct flag as a parameter to denote the condition for the duplicate values in the array.


10:22: to write up the code
03:58: to review the code.

Comments

Post a Comment

Popular posts from this blog

Planting flowers with no adjacent flower plots

Image
Problem Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die. Given a flowerbed (represented as an array containing booleans), return if a given number of new flowers can be planted in it without violating the no-adjacent-flowers rule  Sample inputs  Input: 1,0,0,0,0,0,1,0,0  3 => true  4 => false  Input: 1,0,0,1,0,0,1,0,0  1 => true  2 => false  input: 0  1 => true  2 => false  public boolean canPlaceFlowers(List flowerbed, int numberToPlace) {  // Implementation here  }
Read more
  Given an array of  intervals  where  intervals[i] = [start i , end i ] , merge all overlapping intervals, and return  an array of the non-overlapping intervals that cover all the intervals in the input . Example 1: Input: intervals = [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6]. Example 2: Input: intervals = [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.   Constraints: 1 <= intervals.length <= 10 4 intervals[i].length == 2 0 <= start i <= end i <= 10 4
Read more

Find the maximum number of bomb that can be detonated

  Problem You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb. The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range. You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range.  These bombs will further detonate the bombs that lie in their ranges. Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb. Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So...
Read more