[K9 keyboard problem]Finding the words by ranking - updating
Problem
You have a list of words with ranking.
Now you need to create a function that will take this list as input and provide a way so that a T9 keyboard can provide three top results of probable words based on rankings for the numbers punched in. To help the understanding here is the picture of T9 keyboard.
For example, given the list words with ranking:
We can sort the list of words by rank then search the list to find words matching the keyword. This brute-force approach will result in the following running time.
Sorting : $O(N \log N)$, one time cost
Lookup: $O(N)$
To solve this problem, we need to understand Trie data structure and implement it.
Using the Trie, we can store the input words in each level. Only modification I would make is to remember only Top 3 words.
Once the Trie is built, searching top 3 words starting with given keyword can be found via Tree traverse.
Each node contains the list of top 3 words that share the same prefix and sorted by ranking. (See Figure 1.)
Overall Running is below:
- Building a Trie:
$O(N \log N)$: sorting the list of N words by ranking
$O(K \times N \log N)$: to build the tree, where K is the longest string, N is the number of words given as a input.
- Initializing the T8Keyboard class: $O(1)$
- Searching the words : $O( 4^{I} \times I \times \log N)$
$O(4^I)$: to create the list of possible word combination, where $I$ is the length of key.
$O(4^I \times I \times \log N)$: to find the top 3 words corresponding to each candidate words
$O(N \log N)$ to sort the results by ranking
Therefore, overall running time will be $$O( 4^{I} \times I \times \log N)$$
In the solution, we used the std::map to store the children nodes with a character as a key. It requires $O(\log N)$ to check if there are child with a specified character in each level in the tree.
However, if we use the hash table, in this context a array of node * with size of 256. We can reduce the time to search the candidate words, to $$O(4^I \times I )$$ at an expense of the space, since we need to keep the 256 slots of node * even though only one slot is used.
Here is the complete code.
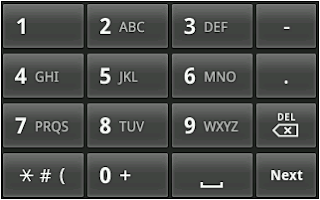 |
| Figure 1: example T9 keyboard |
For example, given the list words with ranking:
[("test", 13), ("tax", 7), ("tom", 50), ("text", 100), ("top", 79),("tub", 101), ("tap", 3))]
Following input from the T9 keyboard, should return the following output.
key = 8: [ (tap, 3)(tax, 7)(test, 13)]
key = 82: [ (tap, 3)(tax, 7)]
key = 83: [ (test, 13)(text, 100)]
key = 86: [ (tom, 50)(top, 79)]
key = 2: [ ]
1. Brute-force approach
We can sort the list of words by rank then search the list to find words matching the keyword. This brute-force approach will result in the following running time.
Sorting : $O(N \log N)$, one time cost
Lookup: $O(N)$
To solve this problem, we need to understand Trie data structure and implement it.
Using the Trie, we can store the input words in each level. Only modification I would make is to remember only Top 3 words.
Once the Trie is built, searching top 3 words starting with given keyword can be found via Tree traverse.
Each node contains the list of top 3 words that share the same prefix and sorted by ranking. (See Figure 1.)
Overall Running is below:
- Building a Trie:
$O(N \log N)$: sorting the list of N words by ranking
$O(K \times N \log N)$: to build the tree, where K is the longest string, N is the number of words given as a input.
- Initializing the T8Keyboard class: $O(1)$
- Searching the words : $O( 4^{I} \times I \times \log N)$
$O(4^I)$: to create the list of possible word combination, where $I$ is the length of key.
$O(4^I \times I \times \log N)$: to find the top 3 words corresponding to each candidate words
$O(N \log N)$ to sort the results by ranking
Therefore, overall running time will be $$O( 4^{I} \times I \times \log N)$$
In the solution, we used the std::map to store the children nodes with a character as a key. It requires $O(\log N)$ to check if there are child with a specified character in each level in the tree.
However, if we use the hash table, in this context a array of node * with size of 256. We can reduce the time to search the candidate words, to $$O(4^I \times I )$$ at an expense of the space, since we need to keep the 256 slots of node * even though only one slot is used.
Here is the complete code.
Comments
Post a Comment