Make the perfect balance on the balances in the room [reviewed]

You have a room-full of balances and weights. Each balance weighs ten pounds and is considered perfectly balanced when the sum of weights on its left and right sides are

exactly the same. You have placed some weights on some of the balances, and you have placed

some of the balances on other balances. Given a description of how the balances are arranged

and how much additional weight is on each balance, determine how to add weight to the balances

so that they are all perfectly balanced.

There may be more than one way to balance everything, but always choose the way that places additional weight on the lowest balances.

The input file will begin with a single integer, N, specifying how many balances there are.

Balance 0 is specified by lines 1 and 2, balance 1 is specified by lines 3 and 4, etc...

Each pair of lines is formatted as follows:

WL

WR

WL and WR indicate the weight added to the left and right sides, respectively.

is a space-delimited list of the other balance that are on that side of this balance.

may contain zero or more elements.

Consider the following input:

4 

0 1 

0 2 

0 

0 3 

3 

0 

0 

0 

Balance 0 has balance 1 on its left side and balance 2 on its right side

Balance 1 has balance 3 on its right side

Balance 2 has three pounds on its left side

Balance 3 has nothing on it

Since balance 3 has nothing on it it is already perfectly balanced, and weighs a total of 10 pounds.

Balance 2 has no other balance on it, so all we need to do is balance it by putting three pounds on its right side. Now it weighs a total of 16 pounds.

Balance 1 has balance three on its right side, which weighs 10 pounds, so we just put 10 pounds on its left side. Balance 1 weighs a total of 30 pounds.

Balance 0 has balance 1 on its left side (30 pounds), and balance 2 on its right side (16 pounds), we can balance it by adding 14 pounds to the right side.

The output should be N lines long, with the nth line listing the weight added to the nth balance, formatted as follows:

So the output for this problem would be:

0: 0 14

1: 10 0

2: 0 3

3: 0 0

Depth First Search through Graph, $O(N)$, N = the number of balances

First of all, understanding the problem took a while (10 mins). After understanding the problem, I realized that the input can be translated into a binary tree or graph.

The example input can be translated into the following graph:

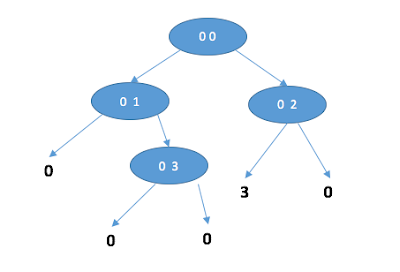Figure 1. graph of balances based on the test input

Once this graph is constructed, we can perform the DFS search and perform the balancing for each node as below:

1. Perform balancing on left and right node.
2. Perform the balancing on the current node.
1. check if current node is balanced. If so, exit.
2. If not, add a weight to lighter side.

It took 27 mins to come up with the algorithm. Spent most of the time defining the class, Balance.
I should've done faster.

Since this DFS only perform balancing on the balance that was not previously visited. Overall running time is $O(N)$

Most of the time spent in writing the code building the graph given input.
Other than that, the main balancing logic did not take long.

Here is the solution in python.


Practice statistics

26:54: to come up with the algorithm
28:30: to write up the complete code.
21:16: to write up the code to parse the input. and fix the bugs (had one bug as a typo and very silly but in the test code. Fixing the later took more than 15 mins).