Decoding numeric string to alphabets.

Problem

Given a string of integers returns the number of ways to decode integers back to Alphabets using the following mapping:

'A' -> 1

'B' -> 2

...

'Z' -> 26

examples:

input = 199

output = 2

explanation:

1-> 9 -> 9 (AII)

11-> 9 (KI)

input = 11

output = 1

explanation:

1->1 (AA)

11 (K)

Answer

Initially, I thought I need to use the conversion table and thought about reversing {key, value} pair to search the alpha for a number. However, it is not necessary because the expected output is just a number of ways to decode numeric strings.

DFS approach

Basically, we need to decide how to tokenize the numeric string and repeat the tokenizing until the end of the string. 

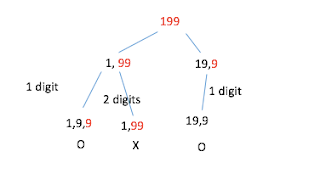
For example 199 we have two ways to tokenize in the beginning:

Each iteration, we move on to the next token and split the next token into either 1 digit and the rest or 2 digits and the rest. 

It is important to understand that the valid range of numbers is between 1 and 26, so anything greater than 26 is not valid so we can stop the searching.

Computing the time complexity is a tricky part since this tree is not an ordinary binary tree. The number of cases decreases each time and ultimately it becomes 1. 

The number of cases we examine is less than $O(2N)$ so it is close to $O(N)$

Here is a solution in python.

Practice statistic

10:00 to write the code

3:00 to fix the 2 bugs (1 in test code and the other in logic)

UPDATE(2022-06-18): Solved the question again. Used DFS with finish condition. This code is much simpler and no need to be mindful of whether we are taking one digit or two digits at all. The finishing condition of checking if the current token is smaller than 27 does the filtering automatically.