Evaluating the mathmatic expression with parentheses

Problem

Given arithmetic equation, 2+(3-1)*4/(5-6), write the program to calculate the result of the equation.

This question is similar to the "Evaluating arithmetic equation", but it is more complicate due to the parentheses.

This problem can be solved using Dijkstra's Shunting-yard algorithm to turn the infix mathematic expression to "Reverse Polish notation", which can be calculated easily.

Conversion of original equation into "Reverse Polish notation", $O(N)$

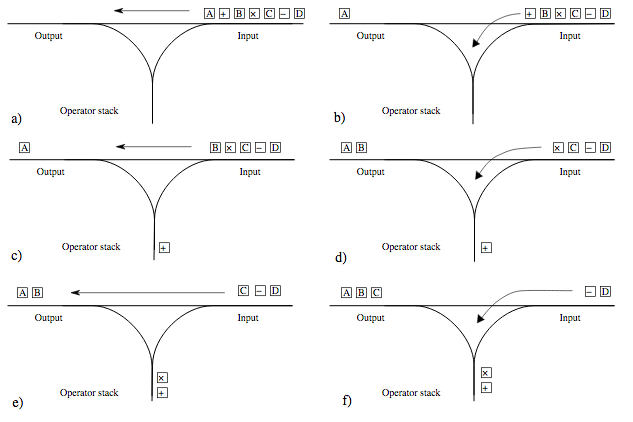
Using the Dijstra's Shunting-yard algorithm, we first need to convert "infix" mathematic equations into "Reverse Polish notations", which can be easily evaluated. (See Figure 1. for the algorithm explanation.)

Figure 1. Graphical illustration of algorithm

Basically, this algorithm keeps one output queue and one stack for the operators.

1. Scan the expression from left to right.

1-1 if  current value is number
      add the value to output queue.

1-2. if current value is arithmetic operator (e.g. +,/,-, *, ^)

      a) if there is any arithmetic operators which priority is greater or equal to the current value.
           pop the operators from the stack and enqueue them into the output queue. (Step D in Figure 1)
      b) push the current value to the stack

1-3) if current value is left parentheses, "("  
         push the parentheses to the stack

1-4) if the current value is right parentheses

         pop all the operators until left parentheses is encountered and put them into the queue.
         pop left parentheses from the stack
2. pop the operators from the stack and put them into the queue.

3. return the queue

This algorithm produce the Reverse polish notations, which can be parsed in the next step.

Evaluate Reverse Polish notations, $O(N)$

We can now evaluate the math expression using the same algorithm in "Evaluating reverse polish notations".

This algorithm is fairly simple to understand and implement.

1. Scan the expression from left to right.

1-1 if the token is number, push it into a stack

1-2 if the token is a operator, pop two numbers from the stack and compute the result.

    push the result into the stack

2. return the final result in the stack.

Running time of this algorithm is $O(N)$, where the N is # of tokens.

Here is the complete code.

Here is another way to parse the expression by examining from the right to left. 

This way does not use Reverse Polish notations. It is a bit more complicated but if you don't remember the reverse polish notation algorithm, you can use it.

This is the reverse polish notation solution in python

UPDATE: 03/31/2022

Solve the question again using Dijkstra's shunting-yarn algorithm. Did not use the python deque. Instead, use the list with pop(0). (in practice, pop(0) takes a $O(N)$ time.  It is easier to understand.

Coding: 37 mins

Debugging: 15 mins (had a bug but could not find it quickly)