Write the algorithm to print valid ways to print parentheses

Problem

Implement an algorithm to print all valid (e.g., properly opened and closed)
combinations of n-pairs of parentheses.
EXAMPLE
Input: 3
Output: ( ( ( ) ) ) , (()()), (())(), ()(()), ()()()


This question took me 54 minutes to solve. I marked it as difficult since I would failed to provide the solution if this question was given for my interview.

However, it might be downgraded to "Medium difficulty" since the algorithm itself is not that complicate.

Depth First with backtracking, $O(2^{2N})$

1. Simply the questions

First we can turn the parentheses into digit that we can compute in the algorithm. Since the pair of parentheses make one complete set, we can assign 1 for "(" and -1 for ")".

2. Find the pattern

Now we have the way to describe the parentheses combination in series of numbers. 
Next step is to capture the pattern that can be translated into algorithm. Let's compare the valid combinations with invalid combinations.

 Valid combinations:

     { 1 1 1 -1 -1 -1 },  {1 -1 1 -1 1 -1},  {1 1 -1 -1 1 -1}

 Invalid combinations:

    {-1 1 -1 1 -1 1, 1} {-1 -1 1 1 -1},  {1 -1 -1 -1 1 1}

Both valid and invalid combination produce the sum of zero at the end. However, valid combination guarantee the accumulative sum in any position in the combination is greater or equal to zero.

It is very subtle but if you examine closely, you will get it. That gives an idea of how we can produce the permutation. 

We can perform the Depth-first-search to find the all the valid combinations of n-pair of parentheses. 
We need to do backtracking to examine all combinations. Criteria to determine whether to proceed with the current combination will be whether the accumulative sum, S $\le$ 0. 

We also need to keep track of the number of right and left parentheses left to use. Let say R is the number of right parentheses and L is the number of left parentheses.

R and L will start from N and -N respectively.
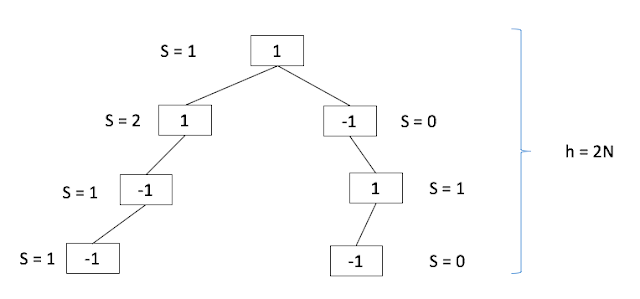Figure 1. illustrate the DFS search when the number of pairs, N = 2.
In each level, we try both 1 and -1 depending on availability of left and right parentheses left.
With the hight of 2N, the running time of this algorithm will be $$O(2^{2N})$$

Here is the complete code.


Practice statistics

27:03: to come up with the algorithm. Finding the pattern took too long.
17:29: to write up the code.
10:01: to validate the algorithm. 1 minor typo


06/24/2019: Retried the same problem.

 Here is python version of solution.
I could use just counter rather than stack for the same result but ran out time.

Practice statistics

35:22:59 : to finish complete coding without error

Comments

Post a Comment

Popular posts from this blog

Planting flowers with no adjacent flower plots

Image
Problem Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die. Given a flowerbed (represented as an array containing booleans), return if a given number of new flowers can be planted in it without violating the no-adjacent-flowers rule  Sample inputs  Input: 1,0,0,0,0,0,1,0,0  3 => true  4 => false  Input: 1,0,0,1,0,0,1,0,0  1 => true  2 => false  input: 0  1 => true  2 => false  public boolean canPlaceFlowers(List flowerbed, int numberToPlace) {  // Implementation here  }
Read more
  Given an array of  intervals  where  intervals[i] = [start i , end i ] , merge all overlapping intervals, and return  an array of the non-overlapping intervals that cover all the intervals in the input . Example 1: Input: intervals = [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6]. Example 2: Input: intervals = [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.   Constraints: 1 <= intervals.length <= 10 4 intervals[i].length == 2 0 <= start i <= end i <= 10 4
Read more

Find the maximum number of bomb that can be detonated

  Problem You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb. The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range. You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range.  These bombs will further detonate the bombs that lie in their ranges. Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb. Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So...
Read more